Area Of Piecewise Rectangular Figure

Expanse of a piecewise rectangular effigy

---

Introduction

In this lesson nosotros notice the area of given piecewise rectangular figures. The figures are broken down into two or more rectangles and their areas are constitute. The sum of the areas of these rectangles gives the expanse of the piecewise rectangular figure.

Consider the following piecewise rectangular figure. We have to detect its area.

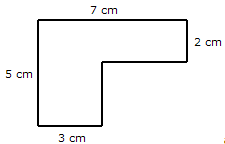
This effigy can be considered as being made of ii rectangles of dimensions vii × 2 and 3 × iii or 5 × 3 and four × 2

Finding the areas of the set up of two rectangles gives the expanse of the piecewise rectangular figure.

Expanse = seven × 2 + 3 × 3 14 + 9 = 23 square units

Area = 5 × three + four × 2 = 15 + 8 = 23 square units

Example one:

Discover the area of piecewise rectangular figure given below.

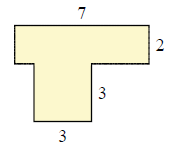
Solution

Step one:

Expanse of a rectangle = l × w; l = length; westward = width

Step 2:

Area of two piecewise rectangles = iii × 3 + 7 × ii = 23 square units

Example 2:

Find the expanse of piecewise rectangular figure given below.

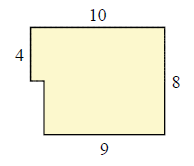
Solution

Step 1:

Expanse of a rectangle = l × w; l = length; due west = width

Step 2:

Area of two piecewise rectangles = 4 × 9 + ten × 4 = 76 foursquare units

Area Of Piecewise Rectangular Figure,

Source: https://www.tutorialspoint.com/perimeter_and_area_of_polygons/area_of_piecewise_rectangular_figure.htm

Posted by: reynaindread.blogspot.com

Share this post